Chapter 9 Calculating Linear Slopes

Citing the Guide and the Package

If you have used smplot2 for your analysis routines, please cite one of the papers below:

Min, S. H. (2024). Visualization of composite plots in R using a programmatic approach and smplot2. Advances in Methods and Practices in Psychological Science, 7(3). [pdf] [codes]
Min, S. H., & Zhou, J. (2021). smplot: an R package for easy and elegant data visualization. Frontiers in Genetics, 12, 802894. [pdf] [codes]

Getting Started

In this chapter, we will use a fake data set, which contains two subject groups (Normal and Amblyopia), as well as experimental conditions (Condition).

Let’s begin by loading the tidyverse and other libraries, and uploading the csv file amblyopia_random.csv using read_csv() from the tidyverse package.

It is always a good habit to make sure that the data set you intended to load uploads properly by using head(), which returns the first 6 rows of the data frame.

library(tidyverse)
library(smplot2)
library(cowplot)
df <- read_csv("https://www.smin95.com/amblyopia_random.csv")
head(df)

## # A tibble: 6 × 5
##   Subject  absBP    SF Group     Condition
##   <chr>    <dbl> <dbl> <chr>     <chr>    
## 1 A1      0.0747   0.5 Amblyopia One      
## 2 A1      0.678    1   Amblyopia One      
## 3 A1      0.868    2   Amblyopia One      
## 4 A1      1.45     4   Amblyopia One      
## 5 A1      0.868    8   Amblyopia One      
## 6 A2      0.237    0.5 Amblyopia One

In this dataset, there are five columns.

First, Subject column has all the subjects. People with amblyopia (a visual disorder) are labelled with A. First subject with amblyopia is written as A1. Normal subject is written with N; first normal subject is N1. We see that there are 10 subjects per group, so there are 20 subjects total.

unique(df$Subject)

##  [1] "A1" "A2" "A3" "A4" "A5" "A6" "A7" "A8" "A9" "N1" "N2" "N3" "N4" "N5" "N6" "N7" "N8" "N9"

Second, absBP is the data of our interest.
Third, SF refers to spatial frequency. We will be calculating slopes of absBP as a function of SF. So these are our x-coordinates for slope calculations (see sections below). Each unit increases by a factor of 2, so it is also helpful to convert the values into log2 units.

length(unique(df$SF))

## [1] 5

df <- df %>% mutate(logSF = log2(SF))
head(df)

## # A tibble: 6 × 6
##   Subject  absBP    SF Group     Condition logSF
##   <chr>    <dbl> <dbl> <chr>     <chr>     <dbl>
## 1 A1      0.0747   0.5 Amblyopia One          -1
## 2 A1      0.678    1   Amblyopia One           0
## 3 A1      0.868    2   Amblyopia One           1
## 4 A1      1.45     4   Amblyopia One           2
## 5 A1      0.868    8   Amblyopia One           3
## 6 A2      0.237    0.5 Amblyopia One          -1

Fourth, Group refers to as the subject gruop. There are two groups: Amblyopia and Normal.

unique(df$Group)

## [1] "Amblyopia" "Normal"

Lastly, Condition refers to the testing condition. In this dataset, there are two conditions.

unique(df$Condition)

## [1] "One" "Two"

The columns Group and Condition are categorical variable and must therefore be factors. head(df) shows that Group and Condition are <chr>, which mean characters. Lets change them to factors <fct>.

df$Group <- factor(df$Group)
df$Condition <- factor(df$Condition)
head(df)

## # A tibble: 6 × 6
##   Subject  absBP    SF Group     Condition logSF
##   <chr>    <dbl> <dbl> <fct>     <fct>     <dbl>
## 1 A1      0.0747   0.5 Amblyopia One          -1
## 2 A1      0.678    1   Amblyopia One           0
## 3 A1      0.868    2   Amblyopia One           1
## 4 A1      1.45     4   Amblyopia One           2
## 5 A1      0.868    8   Amblyopia One           3
## 6 A2      0.237    0.5 Amblyopia One          -1

We see that Group and Condition columns are now factor <fct>.

9.1 Linear relationship using `lm()`

Linear relationship between $x$ and $y$ can be described as $y = mx + b$, where y is the dependent variable, x is the independent variable, m is the slope, and b is the y-intercept.

Let’s try calculate $m$ and $b$ using the data of A3, which is the 3rd amblyopic observer.

A3 <- df %>% filter(Subject == "A3")

There are two conditions here. Let’s filter for data from the second condition only (Condition == Two).

A3_second <- A3 %>% filter(Condition == "Two")

Now, we will use the function lm() to compute $m$ (slope) and $b$ (y-intercept).

In R, the relationship between $y$ (dependent variable) and $x$ (independent variable) is written as y~x using tilde (~). In other words, instead of directly writing $y = mx + b$ in R, we use ~ to describe the relationship between $y$ and $x$. Let’s write the relationship between absBP (dependent variable) and logSF (independent variable) within the function lm().

lm(df$absBP ~ df$logSF)

## 
## Call:
## lm(formula = df$absBP ~ df$logSF)
## 
## Coefficients:
## (Intercept)     df$logSF  
##      0.3134       0.1179

This yields two main outputs. Let’s store this result using a new variable res, which is short for results.

res <- lm(A3_second$absBP ~ A3_second$logSF)
summary(res)

## 
## Call:
## lm(formula = A3_second$absBP ~ A3_second$logSF)
## 
## Residuals:
##       1       2       3       4       5 
##  0.1930 -0.1310 -0.1270 -0.1251  0.1900 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)   
## (Intercept)      0.30461    0.11058   2.755  0.07046 . 
## A3_second$logSF  0.45815    0.06384   7.176  0.00557 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2019 on 3 degrees of freedom
## Multiple R-squared:  0.945,  Adjusted R-squared:  0.9266 
## F-statistic:  51.5 on 1 and 3 DF,  p-value: 0.005574

summary() is a function that prints all the outputs from a given model object. Here, the model object is res, which has been created using the lm() function. When using lm(), it is advisable to always store the results and print the results using summary(). For more information about summary(), please check out ?summary.

We see that the y-intercept $b$ is 0.3046 under the column Estimate. We also see that the slope $m$ is 0.4582 under the column Estimate. You can ignore all the other values for now.

Let’s visualize the data of A3 and fit a linear slope.

A3_second %>% ggplot(aes(x = logSF, y = absBP)) +
  geom_point() +
  geom_abline(slope = 0.4582, intercept = 0.3046)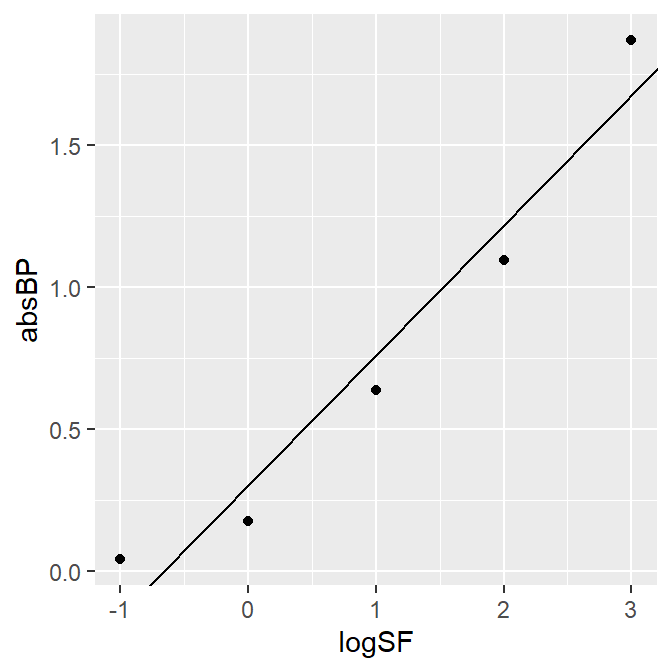

Instead of writing the slope and intercept manually, we can subset these values using $.

res$coefficients

##     (Intercept) A3_second$logSF 
##       0.3046126       0.4581507

The first value is the intercept. Therefore use [[1]] to subset the intercept.

res$coefficients[[1]]

## [1] 0.3046126

You can also subset the slope using [[2]].

res$coefficients[[2]]

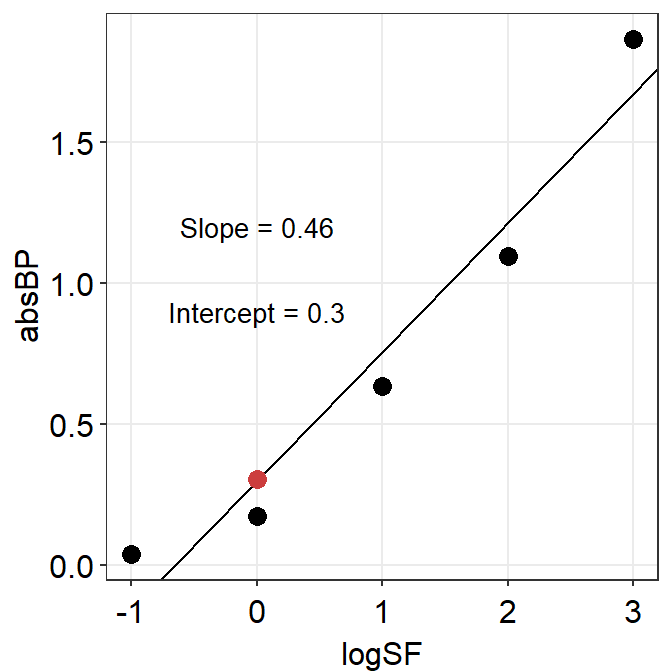
## [1] 0.4581507

Now let’s plot the graph again and label the y-intercept as well. A separate data frame y_int containing the y-intercept is created below. The code below is a bit challenging, so please use ? to figure out each function if you are not sure.

y_int <- data.frame(logSF = 0, absBP = res$coefficients[[1]])

A3_second %>% ggplot(aes(x = logSF, y = absBP)) +
  geom_point(size = 3) +
  geom_abline(
    slope = res$coefficients[[2]],
    intercept = res$coefficients[[1]]
  ) +
  geom_point(data = y_int, color = sm_color("red"), size = 3) +
  sm_hvgrid() +
  annotate("text",
    x = 0, y = 1.2, size = 3.5,
    label = paste("Slope =", round(res$coefficients[[2]], 2))
  ) +
  annotate("text",
    x = 0, y = 0.9, size = 3.5,
    label = paste("Intercept =", round(res$coefficients[[1]], 2))
  )

In summary, you can compute the slope of a linear function between $y$ and $x$ and using lm(), where you use ~ to describe the relationship. You also need to use $ to subset the slopes directly.

9.2 Calculating slopes of all subjects, groups and conditions

Now that we know how to compute slope for each subject, let’s calculate slopes of our entire dataset.

df

## # A tibble: 180 × 6
##    Subject  absBP    SF Group     Condition logSF
##    <chr>    <dbl> <dbl> <fct>     <fct>     <dbl>
##  1 A1      0.0747   0.5 Amblyopia One          -1
##  2 A1      0.678    1   Amblyopia One           0
##  3 A1      0.868    2   Amblyopia One           1
##  4 A1      1.45     4   Amblyopia One           2
##  5 A1      0.868    8   Amblyopia One           3
##  6 A2      0.237    0.5 Amblyopia One          -1
##  7 A2      0.397    1   Amblyopia One           0
##  8 A2      0.813    2   Amblyopia One           1
##  9 A2      0.643    4   Amblyopia One           2
## 10 A2      0.797    8   Amblyopia One           3
## # ℹ 170 more rows

We see that there are 20 subjects total, each of which has completed two conditions. So there are 40 slopes to calculate! Does that mean we need to use lm() 40 times?

The answer is no. smplot has a function sm_slope_all() that returns a dataframe of slopes from linear regression. It works similarly to sm_auc_all().

data = this argument requires the variable that stores the data frame. In our case, it is df.
subjects = this argument requires the name of the column of the data frame that contains subjects. It must strings, ex. 'Subject', not Subject.
groups = this argument requires the name of the column of the data frame that contains each group. In this example, there is no group. An example would be Group column that contains two groups: Normal and Amblyopia.
conditions = this argument requires name of the column of the data frame that contains each condition. In our example, the two conditions are One and Two.
x = this argument requires the name of the column of the data frame that contains the x-axis points from which the AUC can be calculated. In our case, these are values from the logSF column of df. It must be strings, ex. 'logSF', not logSF. Also, it must be numeric/double, NOT factor. Make sure you check that the column is numeric. If its not, convert the column of the dataframe into double beforehand. ex. df$logSF <- as.numeric(df$logSF) or df$SpatialFreq <- as.numeric(df$SpatialFreq).
values = this argument requires the name of the column of the data frame that contains the actual data, which are the y-axis points from which the AUC can be calculated. In our case, it is the change in contrast balance ratio. It must strings, ex. 'absBP', not absBP.

Before using sm_slope_all(), you will need to check for a few things. First, check if the x column is numeric, not factor, by using is.numeric() function. If it is numeric, proceed with using sm_slope_all(). Second, see if the x levels (ex. 0, 3, 6, 12, 24 and 48 etc) are identical for each subject and condition (ex. no 7, 16, 29 minutes for subject 10).

# check if the x column is numeric
is.numeric(df$logSF)

## [1] TRUE

# check if the x column is factor
is.factor(df$logSF)

## [1] FALSE

# if it is factor and not numeric:
df$logSF <- as.numeric(df$logSF)

After checking, we can store the results from sm_slope_all() into a new variable. I will call the new variable slope_df.

slope_df <- sm_slope_all(
  subjects = "Subject",
  conditions = "Condition",
  groups = "Group",
  x = "logSF", values = "absBP",
  data = df
)

## Slope =  absBP  ~  logSF

slope_df

## # A tibble: 36 × 4
##    Subject Condition Group       Slope
##    <chr>   <fct>     <fct>       <dbl>
##  1 A1      One       Amblyopia  0.236 
##  2 A1      Two       Amblyopia  0.283 
##  3 A2      One       Amblyopia  0.137 
##  4 A2      Two       Amblyopia  0.164 
##  5 A3      One       Amblyopia  0.382 
##  6 A3      Two       Amblyopia  0.458 
##  7 A4      One       Amblyopia  0.227 
##  8 A4      Two       Amblyopia  0.272 
##  9 A5      One       Amblyopia -0.0158
## 10 A5      Two       Amblyopia -0.0189
## # ℹ 26 more rows

We see that the slope of A3 in Two condition is identical to the one we have obtained from the lm() function.

res$coefficients[[2]]

## [1] 0.4581507

slope_df %>%
  filter(Subject == "A3" & Condition == "Two") %>%
  select(Slope)

## # A tibble: 1 × 1
##   Slope
##   <dbl>
## 1 0.458

Now we can plot all the slopes from One condition using sm_bar(), sm_boxplot etc. Let’s have a try.

The factor level of slope_df_one$Group is changed below so that bar plot of normal observer is plotted first, then amblyopia (rather than amblyopia -> normals as per alphabetical order).

slope_df_one <- slope_df %>% filter(Condition == "One")
slope_df_one$Group <- factor(slope_df_one$Group,
  levels = c("Normal", "Amblyopia")
)

Here is a boxplot showing slope_df_one’s data.

slope_df_one %>% ggplot(mapping = aes(x = Group, y = Slope, color = Group)) +
  sm_boxplot(
    alpha = 0.6,
    point.params = list(
      size = 2.2,
      alpha = 0.6
    )
  ) +
  scale_color_manual(values = sm_palette(2)) +
  ggtitle("Binocular imbalance")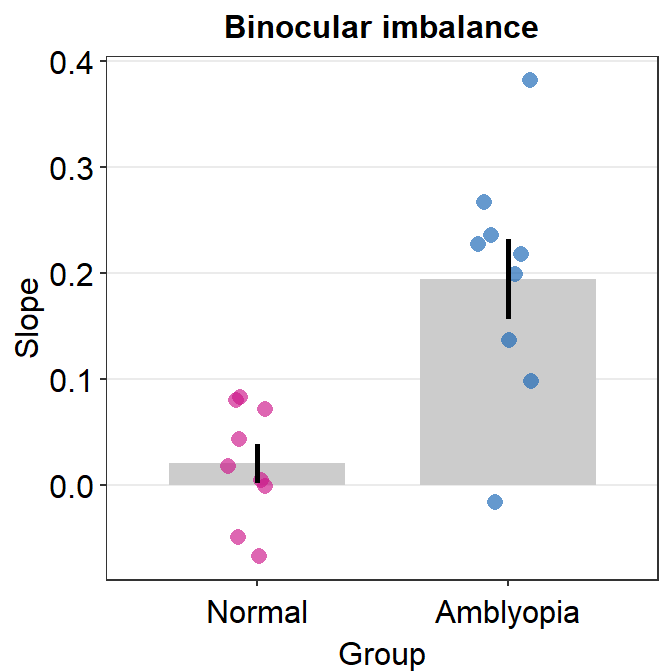

Here is a bar graph showing slope_df’s data for One condition only. This figure is similar to Figure 3B in the paper (Mao et al., 2020).

slope_df_one %>% ggplot(aes(x = Group, y = Slope, color = Group)) +
  sm_bar(shape = 21) +
  scale_color_manual(values = sm_palette(2)) +
  ggtitle("Binocular imbalance")

Chapter 9 Calculating Linear Slopes

Citing the Guide and the Package

Getting Started

9.1 Linear relationship using lm()

9.2 Calculating slopes of all subjects, groups and conditions

9.1 Linear relationship using `lm()`